El Triangulo de Pascal es un triángulo numérico que tiene muchas propiedades y que de el se desprenden un gran numero de curiosidades matemáticas.
En esta ocasión, te mostrare como utilizar el triangulo de Pascal para el Binomio de Newton.
El Binomio de Newton es una fórmula que permite determinar cualquier potencia de un binomio, el cual está formada por una serie de coeficientes que pueden ser determinadas de forma rápida y sencilla a través del siguiente Triángulo de Pascal.

Observa que en todos los extremos del triangulo va escrito el numero 1. Imagina esto como las escaleras de una pirámide formadas por tantos 1 como escalones hasta llegar a la cima.
Luego, para cada fila, cada bloque de números es el resultado de la suma de los dos números que tiene por encima. Por ejemplo, en la fila N° 3 el número 2 es el resultado de la suma de los bloques con números 1 que se ubican encima. Es decir: 1+1=2.
En la fila N°4, los números centrales que son los números 3 están formados por la suma de los bloques superiores, es decir 1+2=3.
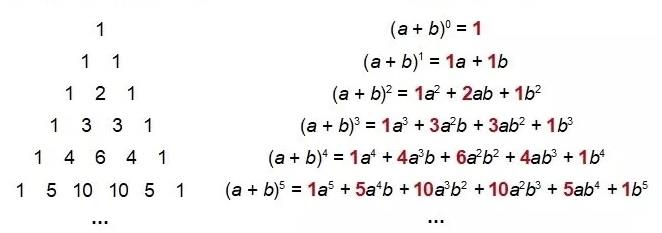
Ahora observa que todos los números correspondientes a una fila son exactamente los mismos coeficientes de la formula del binomio.
Enahorabuena! Ahora ya sabes como utilizar el Triangulo de Pacal como apoyo a tus calculos de binomio.
Bonus
¿Y que pasa con los exponentes? ¿Hay alguna forma de determinarlos? Si, pero ya no es necesario el conocimiento del Triangulo de Pascal, sino de la siguiente formula:

Te lo mostrare con un ejemplo:

Felicidades, ahora seras un experto en resolver problemas de Binomio de Newton.
